Hola.
No me queda claro el tamaño del arreglo L. El i en el punto 2 es la posición en B, ¿no? ¿Puede ser que estés asumiendo que los valores de A y B están en el rango 1 .. n? La letra no lo dice, por lo que el tamaño de L debería ser el de todo el rango de enteros.
Me parece que la solución no es por este camino,
Hay dos ideas que pueden aprovecharse de la letra.
Una es lo de la estrategia similar a QuickSort. Este algoritmo lo vimos en el práctico 7. Lo esencial es él es la partición, que consiste en comparar todos los elementos con un pivote para clasificarlos en dos grupos, el de los menores o iguales al pivote y el de los mayores que el pivote. Hay que tener en cuenta que esta recorrida tiene orden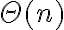
.
La otra es que el tiempo de ejecución debe ser O(n). Teniendo en cuenta que la partición es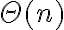 concluimos que la recurrencia no puede ser la clásica 
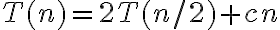porque si fuera así tendríamos 
.
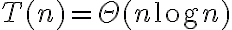Tiene que ser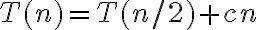
, por lo que al dividir el problema en dos una de las mitades debe poder quedar descartada.
La partición tiene sentido si se aplica a B, porque A ya está ordenado. Queremos partir B en dos grupos iguales o casi iguales. ¿Qué elemento de A, si lo usamos como pivote, nos permite lograr eso sabiendo que los elementos de A y B son los mismos excepto uno? Después de hecha la partición, y sabiendo cuál es la posición en A del elemento elegido como pivote (y por lo tanto los tamaños de los segmentos en que el pivote divide a A), ¿cuáles deben ser los tamaños de los dos grupos en que se partió B? La idea es que con eso puedas decidir en cuál de los dos grupos está el elemento faltante.
¿Ayuda esto?
Saludos,
No me queda claro el tamaño del arreglo L. El i en el punto 2 es la posición en B, ¿no? ¿Puede ser que estés asumiendo que los valores de A y B están en el rango 1 .. n? La letra no lo dice, por lo que el tamaño de L debería ser el de todo el rango de enteros.
Me parece que la solución no es por este camino,
Hay dos ideas que pueden aprovecharse de la letra.
Una es lo de la estrategia similar a QuickSort. Este algoritmo lo vimos en el práctico 7. Lo esencial es él es la partición, que consiste en comparar todos los elementos con un pivote para clasificarlos en dos grupos, el de los menores o iguales al pivote y el de los mayores que el pivote. Hay que tener en cuenta que esta recorrida tiene orden
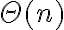. La otra es que el tiempo de ejecución debe ser O(n). Teniendo en cuenta que la partición es
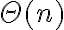concluimos que la recurrencia no puede ser la clásica 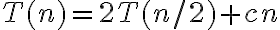porque si fuera así tendríamos 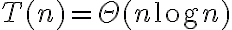.Tiene que ser
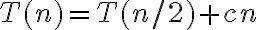, por lo que al dividir el problema en dos una de las mitades debe poder quedar descartada.La partición tiene sentido si se aplica a B, porque A ya está ordenado. Queremos partir B en dos grupos iguales o casi iguales. ¿Qué elemento de A, si lo usamos como pivote, nos permite lograr eso sabiendo que los elementos de A y B son los mismos excepto uno? Después de hecha la partición, y sabiendo cuál es la posición en A del elemento elegido como pivote (y por lo tanto los tamaños de los segmentos en que el pivote divide a A), ¿cuáles deben ser los tamaños de los dos grupos en que se partió B? La idea es que con eso puedas decidir en cuál de los dos grupos está el elemento faltante.
¿Ayuda esto?
Saludos,