Buenas Martina,
Primero te comento que significa "el potencial del centro de la esfera respecto al infinito". Una de las condiciones de borde que se usa para resolver el ejercicio es que o sea que el potencial en el infinito es cero, por lo tanto lo podemos usar como referencia. En otras palabras como que se está pidiendo la diferencia de potencial entre
o sea que el potencial en el infinito es cero, por lo tanto lo podemos usar como referencia. En otras palabras como que se está pidiendo la diferencia de potencial entre 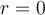 y
y  , pero como en el infinito es cero entonces te están pidiendo directamente cuanto vale el potencial en
, pero como en el infinito es cero entonces te están pidiendo directamente cuanto vale el potencial en 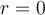 .
.
En la solución lo que se hace entonces es evaluar . El valor de
. El valor de 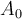 no se calculo previamente porque al calcular el campo eléctrico esa constante no aparece. Por lo tanto la busca hallar aplicando la condición de borde
no se calculo previamente porque al calcular el campo eléctrico esa constante no aparece. Por lo tanto la busca hallar aplicando la condición de borde  , o sea que el potencial es continuo. Aplicando eso con las constantes halladas se ve que
, o sea que el potencial es continuo. Aplicando eso con las constantes halladas se ve que  .
.
Espero te sea de ayuda, si te queda alguna otra duda pregunta sin problemas,
Saludos,
Juan
Primero te comento que significa "el potencial del centro de la esfera respecto al infinito". Una de las condiciones de borde que se usa para resolver el ejercicio es que
 o sea que el potencial en el infinito es cero, por lo tanto lo podemos usar como referencia. En otras palabras como que se está pidiendo la diferencia de potencial entre
o sea que el potencial en el infinito es cero, por lo tanto lo podemos usar como referencia. En otras palabras como que se está pidiendo la diferencia de potencial entre 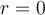 y
y  , pero como en el infinito es cero entonces te están pidiendo directamente cuanto vale el potencial en
, pero como en el infinito es cero entonces te están pidiendo directamente cuanto vale el potencial en 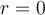 .
.En la solución lo que se hace entonces es evaluar
 . El valor de
. El valor de 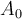 no se calculo previamente porque al calcular el campo eléctrico esa constante no aparece. Por lo tanto la busca hallar aplicando la condición de borde
no se calculo previamente porque al calcular el campo eléctrico esa constante no aparece. Por lo tanto la busca hallar aplicando la condición de borde  , o sea que el potencial es continuo. Aplicando eso con las constantes halladas se ve que
, o sea que el potencial es continuo. Aplicando eso con las constantes halladas se ve que  .
.Espero te sea de ayuda, si te queda alguna otra duda pregunta sin problemas,
Saludos,
Juan