Buenas!
Todos los términos con pasan a ser
pasan a ser 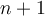 al evaluar
al evaluar 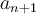 por lo que para aplicar el criterio del cociente calcularíamos el siguiente límite:
por lo que para aplicar el criterio del cociente calcularíamos el siguiente límite:

Si reescribimos un poco este límite obtenemos:

Cancelando los términos que se encuentran en el denominador y en el numerador el problema se reduce a:

Por definición por lo tanto el valor de dicho límite es:
por lo tanto el valor de dicho límite es: 
Saludos!
Florencia
Todos los términos con
 pasan a ser
pasan a ser 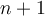 al evaluar
al evaluar 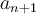 por lo que para aplicar el criterio del cociente calcularíamos el siguiente límite:
por lo que para aplicar el criterio del cociente calcularíamos el siguiente límite:
Si reescribimos un poco este límite obtenemos:

Cancelando los términos que se encuentran en el denominador y en el numerador el problema se reduce a:

Por definición
 por lo tanto el valor de dicho límite es:
por lo tanto el valor de dicho límite es: 
Saludos!
Florencia