Foro de dudas

Buen día.

Hoy en la clase de práctico me preguntaron por este ejercicio. Envío este mensaje para aclarar dudas al respecto, y ya de paso puede servirle a alguien más.

El ejercicio en cuestión pide representar el decimal $num = \dfrac{1}{256}$ en la notación de punto flotante de simple precisión, según el estándar IEEE 754. Aquí le llamé "$num$" de manera arbitraria.
Veamos no solo cómo representarlo en punto flotante, sino también en punto fijo.

De antemano ya sabemos que se trata de un número positivo, con lo cual el bit de signo es 0 (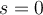$s=0$). Además, su parte entera es nula ($I=0$). 
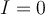Para la parte fraccionaria la idea es observar que $256 = 2^8$ con lo cual se tiene $\frac{1}{256} = 256^{-1} = 2^{-8}$. Con esto, sin hacer ninguna cuenta tenemos que la parte fraccionaria es $F=00000001$.
Así, este número representado en punto fijo con 8 bits tanto para la parte entera como para la parte fraccionaria queda representado como $num=00000000,00000001$.

Ahora, si queremos verlo en punto flotante, ya tenemos 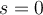$s=0$, resta ver el exponente y la mantisa.
Para el exponente se cumple que $exp=e-127$. Como $exp=0$ al tratarse de un número con parte entera nula: $e=127= 64+32+16+8+4+2+1$. Por lo tanto, en binario con 8 bits tenemos $e=01111111$.
Por otro lado, al tener parte entera nula y parte fraccionaria $F=00000001$, la mantisa es $f=00000001000000000000000$ (recordar que se cuenta con 23 bits para representarla).

Con todo lo anterior tenemos las representaciones tanto en punto fijo como en punto flotante para $num = \frac{1}{256}$.

Cualquier otra consulta no duden en preguntar ya sea en el foro como en las clases de práctico.

Saludos,
Juan Pedro.