Hola. Si 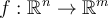 es diferenciable en un punto
es diferenciable en un punto  , el diferencial es la transformación lineal
, el diferencial es la transformación lineal 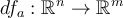 tal que su matriz asociada en la base canónica es
tal que su matriz asociada en la base canónica es 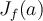 , la matriz Jacobiana de
, la matriz Jacobiana de  en
en  . Por lo tanto, para un
. Por lo tanto, para un 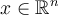 tenemos que
tenemos que 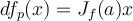 .
.
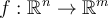 es diferenciable en un punto
es diferenciable en un punto  , el diferencial es la transformación lineal
, el diferencial es la transformación lineal 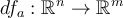 tal que su matriz asociada en la base canónica es
tal que su matriz asociada en la base canónica es 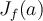 , la matriz Jacobiana de
, la matriz Jacobiana de  en
en  . Por lo tanto, para un
. Por lo tanto, para un 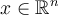 tenemos que
tenemos que 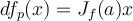 .
.Saludos