Buen día Juan Andrés,
no sé si sigo del todo tu consulta. En las transparencias del teórico se muestra una variante del CFLP donde cada punto de venta se atiende desde un único almacen, por esto las variables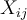 son binarias (o se atiende o no se atiende el punto de venta
son binarias (o se atiende o no se atiende el punto de venta  desde el almacen
desde el almacen 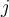 ).
).
En otras variantes, es posible abastecer un único punto de venta desde varios almacenes. En ese caso, lo usual es que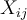 deje de ser binaria, y pase a ser una variable real entre 0 y 1 (si representa la proporción de la demanda de
deje de ser binaria, y pase a ser una variable real entre 0 y 1 (si representa la proporción de la demanda de  abastecida desde
abastecida desde 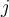 , o una varible positiva cualquiera (si representa, no la proporción de demanda, sino la cantidad absoluta de producto abastecido).
, o una varible positiva cualquiera (si representa, no la proporción de demanda, sino la cantidad absoluta de producto abastecido).
No sé a qué fuentes te referís, como comentaba, hay distintas variantes de problemas similares, y además puede haber muchos modelos alternativos para el mismo problema; cada modelo tiene su "lógica interna", y una restricción aislada es difícil de discutir, sino que más bien es en el conjunto del modelo que tiene sentido.
En particular, si las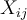 son proporciones (con valores entre 0 y 1), y si obligamos a cubrir el 100% de la demanda, la restricción
son proporciones (con valores entre 0 y 1), y si obligamos a cubrir el 100% de la demanda, la restricción 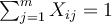 ,
, 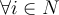 , tiene sentido, porque el 100% de la demanda tiene que ser abastecido sumando las distintas fuentes (almacenes).
, tiene sentido, porque el 100% de la demanda tiene que ser abastecido sumando las distintas fuentes (almacenes).
Lo mismo la restricción (17), parece ser correcta (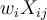 es la cantidad de demanda provista a
es la cantidad de demanda provista a  desde
desde 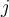 , la suma sobre
, la suma sobre  tiene que ser menor o igual a la capacidad del almacen
tiene que ser menor o igual a la capacidad del almacen 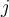 ).
).
Espero esto te ayude. Cualquier duda adicional comentame y tratamos de explicar con más detalle.
Saludos
Héctor
no sé si sigo del todo tu consulta. En las transparencias del teórico se muestra una variante del CFLP donde cada punto de venta se atiende desde un único almacen, por esto las variables
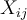 son binarias (o se atiende o no se atiende el punto de venta
son binarias (o se atiende o no se atiende el punto de venta  desde el almacen
desde el almacen 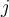 ).
).En otras variantes, es posible abastecer un único punto de venta desde varios almacenes. En ese caso, lo usual es que
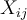 deje de ser binaria, y pase a ser una variable real entre 0 y 1 (si representa la proporción de la demanda de
deje de ser binaria, y pase a ser una variable real entre 0 y 1 (si representa la proporción de la demanda de  abastecida desde
abastecida desde 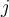 , o una varible positiva cualquiera (si representa, no la proporción de demanda, sino la cantidad absoluta de producto abastecido).
, o una varible positiva cualquiera (si representa, no la proporción de demanda, sino la cantidad absoluta de producto abastecido).No sé a qué fuentes te referís, como comentaba, hay distintas variantes de problemas similares, y además puede haber muchos modelos alternativos para el mismo problema; cada modelo tiene su "lógica interna", y una restricción aislada es difícil de discutir, sino que más bien es en el conjunto del modelo que tiene sentido.
En particular, si las
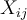 son proporciones (con valores entre 0 y 1), y si obligamos a cubrir el 100% de la demanda, la restricción
son proporciones (con valores entre 0 y 1), y si obligamos a cubrir el 100% de la demanda, la restricción 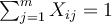 ,
, 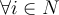 , tiene sentido, porque el 100% de la demanda tiene que ser abastecido sumando las distintas fuentes (almacenes).
, tiene sentido, porque el 100% de la demanda tiene que ser abastecido sumando las distintas fuentes (almacenes).Lo mismo la restricción (17), parece ser correcta (
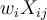 es la cantidad de demanda provista a
es la cantidad de demanda provista a  desde
desde 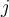 , la suma sobre
, la suma sobre  tiene que ser menor o igual a la capacidad del almacen
tiene que ser menor o igual a la capacidad del almacen 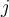 ).
).Espero esto te ayude. Cualquier duda adicional comentame y tratamos de explicar con más detalle.
Saludos
Héctor
