Buenas!
Adjunto aclaración de un error que cometí y que un estudiante me hizo notar respecto al ejercicio 2, parte b, práctico 4. Esencialmente queremos probar que la función en cuestión no es Localmente Lipschitz en un entorno del (0,0). Quedaron además realizados los ajustes correspondientes en los apuntes de clase.
En la clase quisimos ir directamente al (0,0) y ver que no funcionaba allí, pero la definición anda perfecto (observen que la variable t debe quedar fija!)
En (0,0), tenemos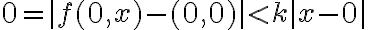 
. No podemos cambiar el valor para la 
.
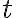Este problema lo resolvemos recordando que para ser localmente Lipschitz, dado un entorno tiene que existir un valor de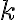 
que funcione para todo el entorno de manera uniforme.
----------------------------------------------------------
Entonces ahora sí, el pique para el ejercicio es tomar una sucesión de puntos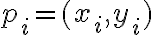 
que se aproxime al (0,0), y de tal forma que:
el valor $K_i$ que necesito para chequear la condición de Lipschitz en el punto $p_i$, tienda a infinito cuando $p_i$ tiende al origen.
Saludos!