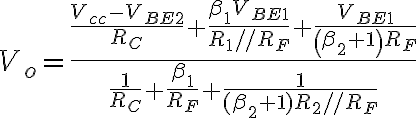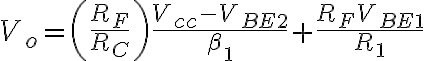Foro del curso

Hola,

El resultado que muestra la solución del práctico está en realidad simplificada.

El resultado exacto (sin despreciar ninguna corriente de base con respecto a corriente de colector, y sin despreciar resistencias mucho más chicas/grandes que otras) da

$V_o=\frac{\frac{ V_{cc} - V_{BE2} }{ R_C } + \frac{ \beta_1 V_{BE1} }{ R_1//R_F }+ \frac{ V_{BE1} }{ \left( \beta_2 + 1 \right) R_F }}{\frac{1}{R_C}+\frac{\beta_1}{R_F}+\frac{1}{(\beta_2+1)R_2//R_F}}$

Al suponer que:

• $\beta_1 \left( \beta_2 + 1 \right) \gg \frac{ R_1//R_F }{ R_F } = 0.053$
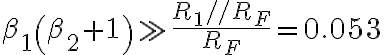
  se puede despreciar el último término del numerador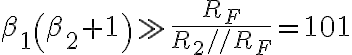
• $\beta_1 \left( \beta_2 + 1 \right) \gg \frac{R_F}{ R_2//R_F} = 101$
  se puede despreciar el último término del denominador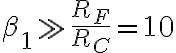
• $\beta_1 \gg \frac{ R_F }{ R_C } = 10$
  se puede despreciar el primer término del denominador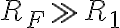
• $R_F \gg R_1$
  se puede aproximar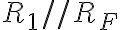 $R_1//R_F$ por $R_1$

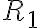
Y nos queda lo que dice la solución del práctico:

$V_o= \left( \frac{ R_F }{ R_C } \right) \frac{ V_{cc} - V_{BE2} }{ \beta_1 } + \frac{ R_F V_{BE1} }{ R_1 }$

Al mirar lo que hiciste, el teorema de Miller parece estar bien planteado.
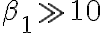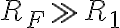No seguí todas las cuentas al detalle (podría haber algún error), pero si aproximas tu resultado usando que $\beta_1 \gg 10$ y que $R_F \gg R_1$ (observar que ambas aproximaciones están listadas arriba), te queda exactamente el resultado de la solución.

Saludos