Hola, Matías. Tu planteo lo veo muy completo y ordenado, y eso es muy importante para poder hacer verificaciones y correcciones.
No estoy completamente seguro de si estás considerando los mismos sistemas de referencia que en la solución publicada.
La razón por la cual no coinciden las velocidades angulares es que tú estás utilizando la velocidad angular de la esfera (o sea, la de un sistema de referencia solidario a la esfera), dada por
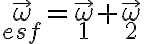
mientras que en la solución hacen el planteo a partir de la velocidad angular de (un sistema solidario a) la varilla, dada esta vez por
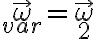 .
.
Por alguna razón le llamaron a esta última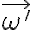 , quizás pensando en la velocidad angular de un sistema relativo que no hay que confundir con la de la esfera.
, quizás pensando en la velocidad angular de un sistema relativo que no hay que confundir con la de la esfera.
Para encontrar las derivadas de los vectores hay que utilizar la velocidad angular del sistema en que se definen. Por eso en la solución tienen
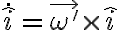 ,
,
etc. Revisa en tu planteo los sistemas de referencia que usas. Si efectivamente usas un sistema solidario a la esfera, la velocidad angular que usaste es la apropiada y la diferencia proviene de un error en alguna otra parte.
Una peculiaridad que, curiosamente, puede provocar confusión es que gracias a su simetría, el tensor de inercia de la esfera con respecto a su centro tiene siempre la misma forma, para cualquier sistema de referencia, ya sea solidario a ésta o no...
Saludos,
NC
No estoy completamente seguro de si estás considerando los mismos sistemas de referencia que en la solución publicada.
La razón por la cual no coinciden las velocidades angulares es que tú estás utilizando la velocidad angular de la esfera (o sea, la de un sistema de referencia solidario a la esfera), dada por
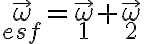
mientras que en la solución hacen el planteo a partir de la velocidad angular de (un sistema solidario a) la varilla, dada esta vez por
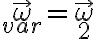 .
.Por alguna razón le llamaron a esta última
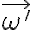 , quizás pensando en la velocidad angular de un sistema relativo que no hay que confundir con la de la esfera.
, quizás pensando en la velocidad angular de un sistema relativo que no hay que confundir con la de la esfera.Para encontrar las derivadas de los vectores hay que utilizar la velocidad angular del sistema en que se definen. Por eso en la solución tienen
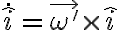 ,
,etc. Revisa en tu planteo los sistemas de referencia que usas. Si efectivamente usas un sistema solidario a la esfera, la velocidad angular que usaste es la apropiada y la diferencia proviene de un error en alguna otra parte.
Una peculiaridad que, curiosamente, puede provocar confusión es que gracias a su simetría, el tensor de inercia de la esfera con respecto a su centro tiene siempre la misma forma, para cualquier sistema de referencia, ya sea solidario a ésta o no...
Saludos,
NC
