Hay dos cuestiones por ahí.
La primera, si la fuente es cosenoidal: Vo.cos(wt) entonces uno, luego de pasar a los complejos, tomará la parte real para encontrar la solución física. Por el contrario, si es senoidal, se tomará la parte imaginaria. Eso viene de la igualdad de Euler: exp(jθ)=cos(θ)+jsen(θ)exp(jθ)=cos(θ)+jsen(θ) .
La otra viene de cómo uno defina la impedancia equivalente. A mi me gusta definirla de esta manera: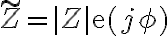
. Por lo que ![\tilde{I}= \frac{\tilde{V}}{\tilde{Z}} = \frac{V_0}{|\tilde{Z}|}\mathrm{exp}(j[\omega t -\phi])](https://eva.fing.edu.uy/filter/tex/pix.php/e5fa1ab1d82e3fcc7bb8b96b5b4c94c5.gif "\tilde{I}= \frac{\tilde{V}}{\tilde{Z}} = \frac{V_0}{|\tilde{Z}|}\mathrm{exp}(j[\omega t -\phi])")
La primera, si la fuente es cosenoidal: Vo.cos(wt) entonces uno, luego de pasar a los complejos, tomará la parte real para encontrar la solución física. Por el contrario, si es senoidal, se tomará la parte imaginaria. Eso viene de la igualdad de Euler: exp(jθ)=cos(θ)+jsen(θ)exp(jθ)=cos(θ)+jsen(θ) .
La otra viene de cómo uno defina la impedancia equivalente. A mi me gusta definirla de esta manera:
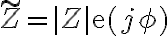. Por lo que Saludos,
Mati