Foro de estudiantes

No entiendo tu duda. Creo que la misma puede estar en el hecho que hay dos flujos diferentes: uno es el flujo en el circuito magnético (llamémosle 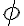$\phi$) y otro es el flujo total por el circuito eléctrico (llamésmole 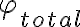$\varphi_{total}$). El que se relaciona con el campo magnético es el primero: 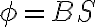$\phi = B S$ donde S es la sección del solenoide. El segundo es 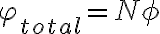$\varphi_{total} = N \phi$, Pero eso está bien discutido en la clase de OpenFing. .

Lo otro que tal vez te genera confusión es que quieras comparar la autoinductancia de un solenoide largo (que deduce en el minuto 50) con la del circuito magnético (que deduce en el minuto 54). Hay que tener cuidado porque ambas expresiones son aproximadas y valen bajo ciertas hipótesis, para poder despreciar en cada caso los efectos de borde. La primera del solenoide largo vale estrictamente para un solenoide infinito (el bobinado se extiende hasta el infinito en ambos extremos), que es la situación en que el campo magnético y la intensidad magnética en el exterior son ambos nulos. Si no se extiende hasta el infinito el campo será chico pero no nulo. En ese caso de solenoide infinito el N/l (que creo es a lo que vos llamás N/a)  que aparece en las expresiones es el número de vueltas por unidad de longitud, Y por eso en los libros del curso deduce la autoinductancia de un toroide, que sería un solenoide largo que se cierra sobre sí mismo.

En el caso del circuito magnético el campo magnético en el exterior es chico pero no nulo, y es por otra razón. Si aplicamos la condición de borde de que las intensidades magnéticas tangenciales son iguales en las regiones que no hay bobinado, me queda que el 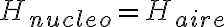$H_{nucleo} = H_{aire}$, que implica 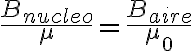$\frac{B_{nucleo}}{ \mu } = \frac{B_{aire}}{ \mu_0 }$. que hace que el campo magnético afuera sea mucho más chico que el de adentro (porque 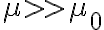$\mu >> \mu_0$), pero la intensidad magnética es igual. Así que al aplicar ampere en un circuito que va por el aire, no se puede despreciar la intensidad magnética en el aire, como se hace en el solenoide largo. Además la bobina no es infinita, porque solo está en un tramo del circuito.

Ahora, podríamos comparar la expresión de un circuito magnético que tenga un entrehierro grande con el del solenoide infinito. En ese caso la inductancia con un entrehierro grande queda 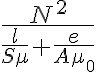$\frac{N^2}{ \frac{l}{S \mu } + \frac{e}{A \mu _0} }$, donde e es el largo del entre hierro y A su sección. Si el entrehierro es chico A = S. pero si es grande no porque las líneas de campo se van a doblar. Para un entrehierro muy grande e tiende a infinito, pero también A tiende a infinito. Y gana este último porque eso hace que el campo magnético en el exterior tienda a cero como en el caso del solenoide (se cumple 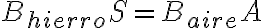$B_{hierro} S = B_{aire} A$). Luego el segundo término en el denominador de la autoinductancia es despreciable y 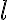$l$ sería el largo del hierro, que para poder compararlo con el del solenoide, como la bobina tiene que ser infinita, será aproximadamente el largo de la bobina. Y ahí si recuperamos el mismo resultado en ambos casos.

Bueno, no sé si esta era tu duda. Si no lo era, por favor aclará un poco mejor cuál era.