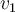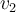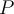Hola me podrían ayudar con este ejercicio?
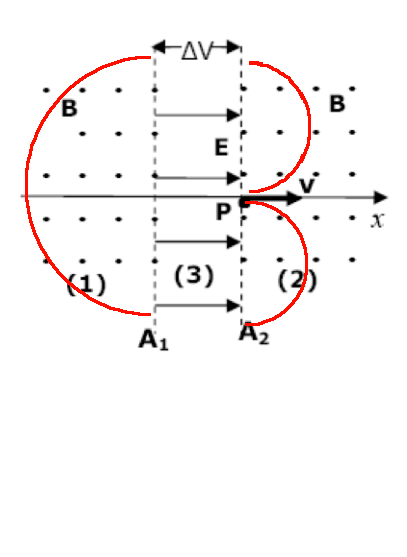
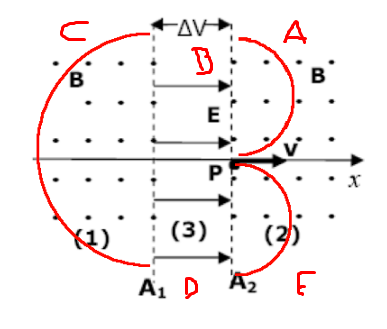
Entiendo que electrón realiza un movimiento semicircular al inicio de modo que entra a la zona donde esta el campo eléctrico para luego salir y realizar otro movimiento semicircular, pero luego no puede entrar ya que la fuerza eléctrica es opuesta al sentido del campo lo que impide al electrón avanzar.
No se que relacion puedo aplicar para solución ar el problema.
Intente hallar las velocidades en cada instante en relacion con DV=-1/q*Wa-b.
Gracias y disculpen las molestias.