Foro de consultas generales

Buenos días, Ignacio. La base del argumento es mostrar que la normal es perpendicular a la velocidad, y que por lo tanto la potencia de la normal es nula.

Hay varios caminos equivalentes para mostrar que esto es así. En la solución ofrecida en la página, se define un versor 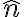$\hat n$ orientado según la dirección normal al paraboloide. La fuerza normal apunta según esta dirección. La partícula se mueve sobre la superficie del paraboloide, y en la solución esto se representa al escribir el vector la velocidad como la suma de una componente en dirección 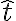$\hat t$ (contenida en un plano vertical) y otra en dirección $\hat e _\varphi$ (contenida en un plano horizontal), ambas perpendiculares a la normal.

Otra posibilidad, un poco más larga, sería escribir las componentes de los vectores en coordenadas cilíndricas, digamos, y mostrar que la normal y la velocidad son perpendiculares usando estas expresiones. La idea sería más o menos así: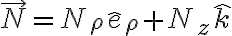
$\vec N = N_\rho \hat e_\rho + N_z \hat k$  (la normal no tiene componente según $\hat e_\varphi$).
$\vec v = v_\rho \hat e_\rho + v_z \hat k + v_\varphi \hat e _\varphi$

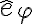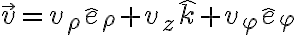
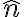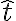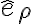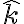(observemos que tanto $\hat n$ como $\hat t$ se pueden escribir como combinaciones lineales de $\hat e_\rho$ y $\hat k$). Entonces,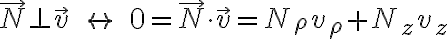
$\vec N \perp \vec v \quad \leftrightarrow \quad 0=\vec N \cdot \vec v = N_\rho v_\rho + N_z v_z$

(esto equivale a decir que 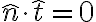$\hat n \cdot \hat t = 0$). Si ahora usamos la forma de la velocidad en coordenadas cilíndricas en la última expresión, tenemos que demostrar que se cumple la igualdad

$N_\rho \dot \rho + N_z \dot z = 0$

Una de las formas de proceder es tomar en cuenta la expresión 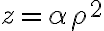$z=\alpha \rho^2$ para establecer relaciones entre las componentes de la normal por un lado, y entre las derivadas de las coordenadas por otro (p.ej. $\dot z = 2\alpha \rho \dot \rho$)...

---

Hay más posibilidades válidas para hacer la demostración, pero en última instancia en todos los casos hay que probar $\vec N \cdot \vec v = 0$. Notemos que hay que vigilar que estemos planteando correctamente las direcciones de los vectores; por ejemplo, no hay que asumir que la velocidad (o la normal) sea horizontal en general.

En la mayoría de los ejercicios y situaciones planteadas nos vamos a encontrar con que la normal sobre una partícula que se mueve sobre una superficie es de potencia nula, ya que, por definición, su dirección es perpendicular a la superficie y podemos aplicar el razonamiento anterior en forma análoga. Pero, ¿es siempre así? ¿puede pasar que la normal sobre la partícula tenga potencia no nula? En caso afirmativo, ¿cuál podría ser un ejemplo? De lo contrario, ¿cómo se puede hacer la demostración?

----

Saludos,

NC