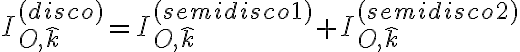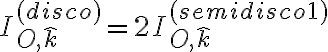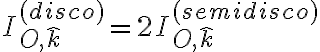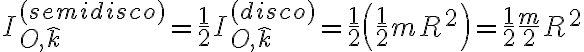Hola Francisco,
(antes que nada podés ver la versión ampliada hecha sólo por cardinales, en la pág. 2 hay algo al respecto de tu duda)
como se trata de un problema de dinámica en el plano, lo que necesitás en este ejercicio es el momento de inercia del semidisco con respecto a un eje perpendicular al plano 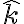 y que pase por un punto de interés, digamos
y que pase por un punto de interés, digamos  :
: 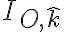 .
.
Consideremos un disco homogéneo de centro  , radio
, radio  y masa
y masa 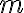 , para el que sabemos que
, para el que sabemos que 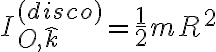 .
.
Como el momento de inercia (el tensor mismo en realidad) es aditivo en la masa del sistema, podemos suponer que corresponde a la contribución de 2 semidiscos, llamémosle 1 y 2, de igual radio y cada uno de masa 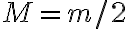 :
:
pero el rol de cada semidisco es igual, por lo que:
y saquemos la nomenclatura de 1 y 2 que no tiene sentido a esta altura:
de donde podemos despejar el momento de inercia de interés:
y usando que la masa 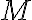 del semidisco es
del semidisco es 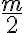 , nos queda:
, nos queda:
Saludos,
Ariel.