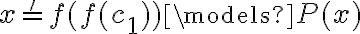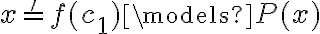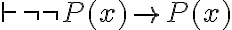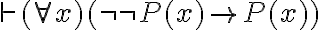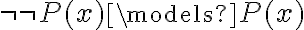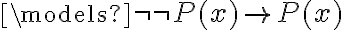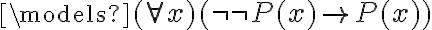Teórico de Semántica - Lógica de Primer Orden

Hola.

Como toda pregunta, hay dos respuestas: una corta y una larga :-) .

Voy a tratar de explicar el problema. Sigo con la política que pusiste que me parece buena: para fijar ideas usamos 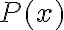$P(x)$ pero podría ser 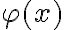$\varphi(x)$, asumiendo $x$ libre.

El primer punto es hacerse la siguiente pregunta: "Puedo calcular 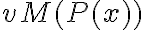$v^\mathcal{M}(P(x))$ con la definición?"

La respuesta clara es: no se puede calcular porque la definición la interpretación está dada sólo para sentencias y no para fórmulas con variables libres. Eso significa que si tengo variables libres no puedo aplicar la función.

Sin embargo, por qué es así?

Si alguien (El Preguntón :-)¹ ) le pregunta a Juan :

(Preguntón :-) ): Cuánto es $x+5$ ?.

nuestra respuesta debería ser otra pregunta:

(Juan): Cuanto vale $x$?.

El problema es esencialmente el mismo. El diálogo sería:

(P) Cuál es el valor de verdad de 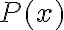$P(x)$ en $\mathcal{M}=\langle N, Pares, suc, 0 \rangle$?

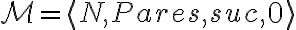(J) Para que Natural?

El primer punto es que no podemos pensar en 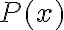$P(x)$ en abstracto. Tenemos que pensar en 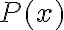$P(x)$ en un contexto. La pregunta de Juan es para determinar el contexto en el cual interpretar esa fórmula.

Para poder trabajar con estas fórmulas (con variables libres), lo que se hace es tomar la convención de que  $x$ es cualquier elemento del dominio . Esto es que el valor de verdad es el mismo en cualquier elemento del dominio.

Esto es sólo una convención. Aunque la realidad es más compleja. Para verlo, pensemos en la siguiente afirmación:

$x='f(f(c_1)) \models P(x)$

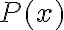En este caso, $x$ ya no es cualquier elemento del dominio. Hay un contexto que está dado por la hipótesis: $x$ es el natural 2. En este contexto, podemos afirmar ahora que $P(x)$ es verdadero y por lo tanto el juicio anterior también lo es. Si la afirmación fuera:

$x='f(c_1) \models P(x)$

tendríamos que decir que el juicio es falso porque 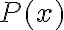$P(x)$ es falso cuando $x$ es 1.

Conclusión: Las fórmulas con variables libres necesitan de un contexto para ser interpretadas. Ese contexto está dado por valores del dominio para cada una de sus variables libres. Cuando no se conocen esos valores, entonces se asume cuantificación universal.

El libro de Van Dalen, cuando considera la consecuencia lógica ( 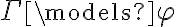$\Gamma \models \varphi$ ), asume que las hipótesis son solamente sentencias, con lo cual se soluciona el problema y siempre hay que clausurar.

Cuando se va a demostrar corrección, allí el libro levanta la restricción y redefine la noción de consecuencia lógica de forma de soportar en las hipótesis fórmulas que tengan variables libres.

La idea de clausurar surge un poco de esa idea de que las hipótesis son sólo sentencias.

Espero que se entienda la idea.

Igual, el tipo este :-) sigue preguntando :

(P): Cuál es la diferencia entre las siguientes tres afirmaciones?

• $\neg \neg P(x) \vdash P(x)$
  
• $\vdash \neg \neg P(x) \to P(x)$
  
• $\vdash (\forall x) (\neg \neg P(x) \to P(x))$
  

(P): Y entre las siguientes tres?

• $\neg \neg P(x) \models P(x)$
• $\models \neg \neg P(x) \to P(x)$
  
• $\models (\forall x) (\neg \neg P(x) \to P(x))$
  

Saludos a todos.

FDO.