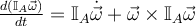Hola,
al plantear la derivada del momento angular (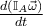 ) como:
) como:
estás usando que expresás tanto el tensor de inercia como la velocidad angular en un sistema solidario al rígido (ver la observación que sigue a ec. (8.3) en los Apuntes 2010); esta forma de derivar es sin dudas útil, pero depende de usar un sistema adecuado para acompañar al rígido.
El problema es que la base que utilizás para expresar el tensor de inercia y la velocidad angular corresponde a un sistema que no es solidario al rígido ya que ni 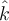 ni
ni 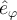 lo acompañan, pero el tensor no cambia visto desde allí!: por ejemplo, los momentos de inercia con respecto a cada eje no cambian aunque gire el disco, se ven igual desde cada uno de estos ejes (todo gracias a la simetría de revolución del rígido, claro). Esa base es entonces muy buena para trabajar! por lo que no tenés que cambiarla, sino derivar correctamente:
lo acompañan, pero el tensor no cambia visto desde allí!: por ejemplo, los momentos de inercia con respecto a cada eje no cambian aunque gire el disco, se ven igual desde cada uno de estos ejes (todo gracias a la simetría de revolución del rígido, claro). Esa base es entonces muy buena para trabajar! por lo que no tenés que cambiarla, sino derivar correctamente:
la mejor alternativa desde mi punto de vista es calcular el momento angular 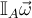 y derivar correctamente su expresión (es como está hecho en la solución, el único versor a derivar es
y derivar correctamente su expresión (es como está hecho en la solución, el único versor a derivar es 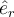 pero te sale fácilmente).
pero te sale fácilmente).
Saludos,
Ariel.