Hola. Ayer me preguntaron sobre el desarrollo de Laurent de 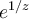 y respondí cualquier cosa, porque me puse a hablar de la derivada en infinito, pero acá la singularidad en cuestión es en z=0 (que según recuerdo la pregunta era de qué tipo de singularidad se trataba). Pido disculpas, y explico abajo por qué se trata de una singularidad esencial. Cualquier duda me vuelven a preguntar.
y respondí cualquier cosa, porque me puse a hablar de la derivada en infinito, pero acá la singularidad en cuestión es en z=0 (que según recuerdo la pregunta era de qué tipo de singularidad se trataba). Pido disculpas, y explico abajo por qué se trata de una singularidad esencial. Cualquier duda me vuelven a preguntar.
La expresión 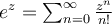 es valida para todo
es valida para todo 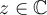
En particular en el anillo 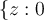 , (\ e^{1/z} \) se puede calcular sustituyendo
, (\ e^{1/z} \) se puede calcular sustituyendo 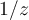 en la fórmula de arriba. Por unicidad de la serie de Laurent, esa serie es el desarrollo de Laurent de (\ e^{1/z}\) en el anillo
en la fórmula de arriba. Por unicidad de la serie de Laurent, esa serie es el desarrollo de Laurent de (\ e^{1/z}\) en el anillo 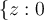 , y por lo tanto la singularidad en 0 es esencial.
, y por lo tanto la singularidad en 0 es esencial.