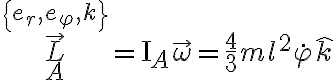en la parte c), en el resultado aparece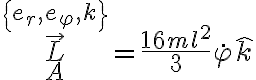 
que sería el momento angular de la barra AB respecto a A pero a mi me da esto:
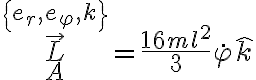que sería el momento angular de la barra AB respecto a A pero a mi me da esto:
La base es la solidaria a la barra AB.
Y lo que no entiendo es de dónde sale el 16.
Los otros términos del momento angular total coinciden con el momento angular de la barra BC respecto a la misma base...
Salu2