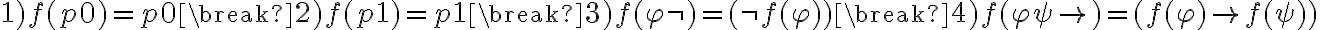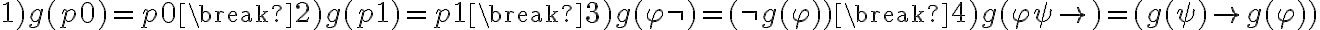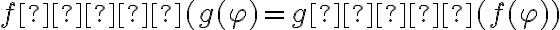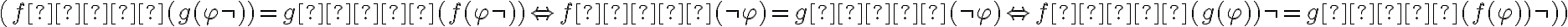Parciales

Hola, en el ejercicio 1, partes b y c. se pide que construya dos funciones recursivas f y g. Tomando en cuenta estas definiciones, luego en la parte d se pide demostrar que 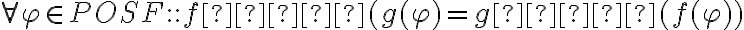$\forall \varphi \in POSF :: f⁻¹ (g( \varphi ) = g⁻¹(f(\varphi))$

Llegue en la parte b que f está definida:

$1) f(p0) = p0 \break 2) f(p1) = p1 \break 3) f(\varphi \neg ) = (\neg f(\varphi)) \break 4) f(\varphi \psi \rightarrow) = ( f(\varphi) \rightarrow f(\psi))$

y en la parte c que g está definida: 

$1) g(p0) = p0 \break 2) g(p1) = p1 \break 3) g(\varphi \neg ) = (\neg g(\varphi)) \break 4) g(\varphi \psi \rightarrow) = ( g(\psi) \rightarrow g(\varphi))$

Son correctas estas definiciones?

Porque tomando en cuenta estas mismas y las de f^(-1) y g^(-1), para demostrar la parte d, en el primer caso inductivo, tratando de demostrarla para 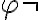$\varphi \neg$ llego a lo siguiente:

Tomando como hipótesis que $f⁻¹(g(\varphi) = g⁻¹(f(\varphi))$

$\( f⁻¹(g(\varphi \neg)) = g⁻¹(f(\varphi \neg)) \Leftrightarrow f⁻¹(\neg \varphi) = g⁻¹(\neg \varphi) \Leftrightarrow f⁻¹(g(\varphi))\neg = g⁻¹(f(\varphi)) \neg ))$ \)

Sería correcta esa forma de encararlo?

Gracias