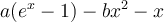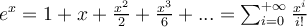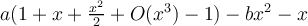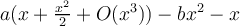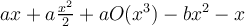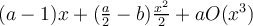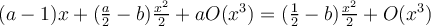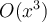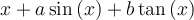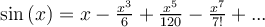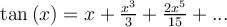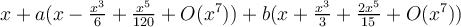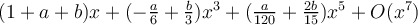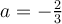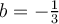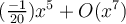Desarrollo de Taylor de 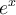 en el entorno de
en el entorno de 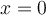 :
:
Entonces se tiene
Para eliminar el término en  , se elige
, se elige 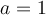 :
:
Para eliminar el término en 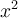 , se elige
, se elige 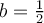 :
:
Desarrollo de Taylor de 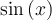 en el entorno de
en el entorno de 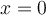 :
:
Desarrollo de Taylor de 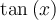 en el entorno de
en el entorno de 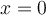 :
:
Entonces se tiene
Buscamos que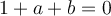 y
y 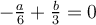
Nos queda un infinitésimo de orden 5.