Diagrama de temas

  • TOPOLOGÍA Y ANÁLISIS REAL

    - 1er Semestre de 2024 -



    Idea y objetivos generales del curso: 


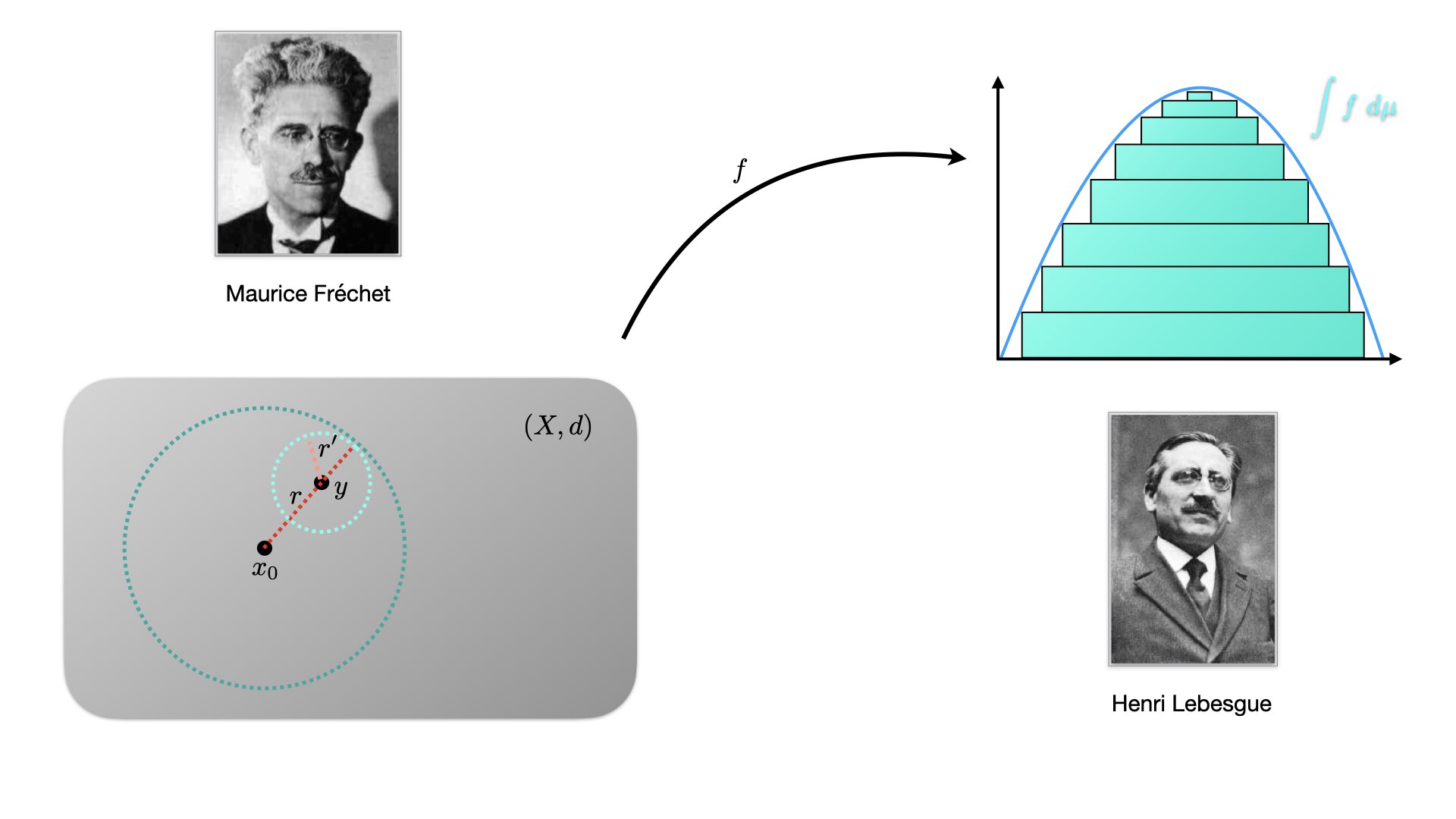
    Podemos pensar a grosso modo que los tres conceptos fundamentales del cálculo son la continuidad, la integración y la diferenciabilidad. En este curso, haremos una revisita formal y un abordaje más general a estos tres conceptos. Específicamente, la continuidad de funciones de variable real se extenderá a funciones con valores reales definidas sobre espacios métricos. Recuerde que en los cursos anteriores de cálculo, se nos daba una función continua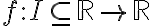 f \colon I \subseteq \mathbb{R} \to \mathbb{R} y nos preguntaban posibles propiedades de f (por ejemplo, ¿f es acotada?, ¿alcanza máximo y mínimo?). 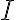En algunos casos, se puede responder afirmativamente a estas cuestiones dependiendo de la estructura de I, por ejemplo cuando 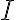I es un intervalo compacto (cerrado y acotado). 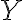En este curso, estas y otras cuestiones, además de ser revisitadas y probadas de manera más general, vendrán acompañadas de otro enfoque, a saber, si tenemos una función continua f entre espacios métricos X e Y, ¿qué podemos decir de la estructura de X a partir de una o varias propiedades de f?. En la segunda parte del curso se estudiará la integral de Lebesgue, un tipo de integral más general que la integral de Riemann (en el sentido que toda función integrable según Riemann lo será según Lebesgue, pero además hay funciones integrables según Lebesgue que no lo son según Riemann). 


    Número de créditos: 

    10 créditos.


    Metodología de enseñanza:

    Clases teóricas (52 horas) 

    Clases prácticas (23 horas). 

    Las clases teóricas consistirán en exposiciones del docente. En los espacios destinados al práctico se espera que los estudiantes piensen problemas propuestos en los repartidos, con guía del docente. En cuanto a la dedicación no presencial, se espera que el estudiante destine horas a la revisión de los contenidos vistos en clases, resolución de problemas (ya sean de los repartidos o de otras fuentes), entrega de tareas y preparar una exposición oral. 


    Conocimientos previos exigidos y recomendados: 

    Nociones de cálculo diferencial e integral en una y varias variables, álgebra lineal. 

    Pueden ser de utilidad conocimientos en ecuaciones diferenciales.
►Docente, horarios y salones