3. Formalismo y algoritmos sencillos
Perfilado de sección
-
Estados cuánticos como vectores complejos y compuertas cuánticas como matrices unitarias. Matrices de Pauli. Autoestados. Algoritmos básicos (Deutsch-Jozsa, Simon). Notación de Dirac.
Posibles referencias: para números complejos y álgebra lineal, el capítulo 1 del Yanofsky-Manucci; sobre producto tensorial, la sección 2.7 del Yanofsky-Manucci; para álgebra lineal y notación de Dirac, el Apéndice A del libro de Mermin, la sección 2.1 del Nielsen-Chuang, la sección 2.3 del Benenti-Casati-Strini, o cualquier otra fuente confiable que les resulte útil. Los algoritmos están en casi cualquier texto de información cuántica; sugiero mirar el libro de Mermin luego de aprender notación de Dirac (el Nielsen-Chuang tiene todo, pero es más difícil de seguir porque lo plantea a un nivel más abstracto).
-
Práctico 3 Archivo
-
Diapos primera clase Práctico 3 Archivo
-
Clases grabadas Página
-
Dado el estado de la figura (que ya está normalizado, verificarlo!), si medimos el círculo, indicar la probabilidad de que el resultado sea "negro":

-
Considere un estado no clásico de tres qubits correspondiente a la superposición coherente de dos estados clásicos en la forma:
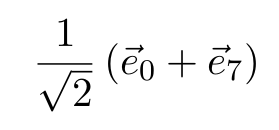
Indicar cuál de las afirmaciones es correcta:
(a) El estado es autoestado de X ⊗ X ⊗ X con valor propio - 1.
(b) El estado es autoestado de X ⊗ X ⊗ X con valor propio + 1.
(c) El estado es autoestado de Z ⊗ Z ⊗ Z con valor propio - 1.
(d) El estado es autoestado de Z ⊗ Z ⊗ Z con valor propio + 1.
